13.6: Volume Between Surfaces and Triple Integration |
您所在的位置:网站首页 › z=0 z=y y=1 › 13.6: Volume Between Surfaces and Triple Integration |
13.6: Volume Between Surfaces and Triple Integration
|
We learned in Section 13.2 how to compute the signed volume \(V\) under a surface \(z=f(x,y)\) over a region \(R\): \(V = \iint_R f(x,y) dA\). It follows naturally that if \(f(x,y)\geq g(x,y)\) on \(R\), then the volume between \(f(x,y)\) and \(g(x,y)\) on \(R\) is \[ \begin{align} V &= \iint_R f(x,y) dA - \iint_R g(x,y) dA \\[4pt] &= \iint_R \big(f(x,y)-g(x,y)\big) dA. \end{align} \] theorem 124: Volume Between Surfaces Let \(f\) and \(g\) be continuous functions on a closed, bounded region \(R\), where \(f(x,y)\geq g(x,y)\) for all \((x,y)\) in \(R\). The volume \(V\) between \(f\) and \(g\) over \(R\) is \[V =\iint_R \big(f(x,y)-g(x,y)\big) dA.\] Example \(\PageIndex{1}\): Finding volume between surfaces Find the volume of the space region bounded by the planes \(z=3x+y-4\) and \(z=8-3x-2y\) in the \(1^\text{st}\) octant. In Figure 13.36(a) the planes are drawn; in (b), only the defined region is given. Solution We need to determine the region \(R\) over which we will integrate. To do so, we need to determine where the planes intersect. They have common \(z\)-values when \(3x+y-4=8-3x-2y\). Applying a little algebra, we have: \[\begin{align*} 3x+y-4 &= 8-3x-2y\\ 6x+3y &=12\\ 2x+y &=4 \end{align*}\] The planes intersect along the line \(2x+y=4\). Therefore the region \(R\) is bounded by \(x=0\), \(y=0\), and \(y=4-2x\); we can convert these bounds to integration bounds of \(0\leq x\leq 2\), \(0\leq y\leq 4-2x\). Thus \[\begin{align*} V &= \iint_R \big(8-3x-2y-(3x+y-4)\big) dA \\ &= \int_0^2\int_0^{4-2x} \big(12-6x-3y\big) dy \, dx\\ &= 16\text{u}^3. \end{align*}\] The volume between the surfaces is \(16\) cubic units. 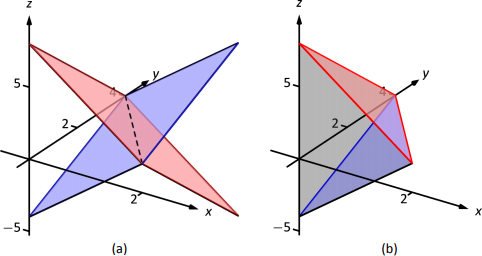 Figure 13.36: Finding the volume between the planes given in Example 13.6.1. Figure 13.36: Finding the volume between the planes given in Example 13.6.1.
In the preceding example, we found the volume by evaluating the integral \[ \int_0^2\int_0^{4-2x} \big(8-3x-2y-(3x+y-4)\big) dy \, dx.\] Note how we can rewrite the integrand as an integral, much as we did in Section 13.1: \[8-3x-2y-(3x+y-4) = \int_{3x+y-4}^{8-3x-2y} dz.\] Thus we can rewrite the double integral that finds volume as \[\int_0^2\int_0^{4-2x} \big(8-3x-2y-(3x+y-4)\big) dy \, dx = \int_0^2\int_0^{4-2x}\left(\int_{3x+y-4}^{8-3x-2y} dz\right) dy \, dx.\] This no longer looks like a "double integral,'' but more like a "triple integral.'' Just as our first introduction to double integrals was in the context of finding the area of a plane region, our introduction into triple integrals will be in the context of finding the volume of a space region. To formally find the volume of a closed, bounded region \(D\) in space, such as the one shown in Figure 13.37(a), we start with an approximation. Break \(D\) into \(n\) rectangular solids; the solids near the boundary of \(D\) may possibly not include portions of \(D\) and/or include extra space. In Figure 13.37(b), we zoom in on a portion of the boundary of \(D\) to show a rectangular solid that contains space not in \(D\); as this is an approximation of the volume, this is acceptable and this error will be reduced as we shrink the size of our solids. The volume \(\Delta V_i\) of the \(i^\text{th}\) solid \(D_i\) is \(\Delta V_i = \Delta x_i\Delta y_i\Delta z_i\), where \(\Delta x_i\), \(\Delta y_i\) and \(\Delta z_i\) give the dimensions of the rectangular solid in the \(x\), \(y\) and \(z\) directions, respectively. By summing up the volumes of all \(n\) solids, we get an approximation of the volume \(V\) of \(D\): $$V \approx \sum_{i=1}^n \Delta V_i = \sum_{i=1}^n \Delta x_i\Delta y_i\Delta z_i.\] Let \(||\Delta D||\) represent the length of the longest diagonal of rectangular solids in the subdivision of \(D\). As \(||\Delta D||\to 0\), the volume of each solid goes to 0, as do each of \(\Delta x_i\), \(\Delta y_i\) and \(\Delta z_i\), for all \(i\). Our calculus experience tells us that taking a limit as \(||\Delta D||\to 0\) turns our approximation of \(V\) into an exact calculation of \(V\). Before we state this result in a theorem, we use a definition to define some terms. Definition 106: Triple Integrals, Iterated Integration (Part I) Let \(D\) be a closed, bounded region in space. Let \(a\) and \(b\) be real numbers, let \(g_1(x)\) and \(g_2(x)\) be continuous functions of \(x\), and let \(f_1(x,y)\) and \(f_2(x,y)\) be continuous functions of \(x\) and \(y\). The volume \(V\) of \(D\) is denoted by a triple integral, $$V = \iiint_D dV.$$ The iterated integral \( \int_a^b\int_{g_1(x)}^{g_2(x)}\int_{f_1(x,y)}^{f_2(x,y)} dz \, dy \, dx\) is evaluated as $$\int_a^b\int_{g_1(x)}^{g_2(x)}\int_{f_1(x,y)}^{f_2(x,y)} dz \, dy \, dx=\int_a^b\int_{g_1(x)}^{g_2(x)}\left(\int_{f_1(x,y)}^{f_2(x,y)} dz\right) dy \, dx.$$ Evaluating the above iterated integral is triple integration.Our informal understanding of the notation \(\iiint_D dV\) is "sum up lots of little volumes over \(D\),'' analogous to our understanding of \(\iint_R dA\) and \(\iint_R\ dm\). We now state the major theorem of this section. theorem 125 Triple Integration (Part I) Let \(D\) be a closed, bounded region in space and let \(\Delta D\) be any subdivision of \(D\) into \(n\) rectangular solids, where the \(i^\text{th}\) subregion \(D_i\) has dimensions \(\Delta x_i\times\Delta y_i\times\Delta z_i\) and volume \(\Delta V_i\). The volume \(V\) of \(D\) is $$V = \iiint_D dV = \lim_{||\Delta D||\to0} \sum_{i=1}^n \Delta V_i = \lim_{||\Delta D||\to0} \sum_{i=1}^n \Delta x_i\Delta y_i\Delta z_i.$$ If \(D\) is defined as the region bounded by the planes \(x=a\) and \(x=b\), the cylinders \(y=g_(x)\) and \(y=g_2(x)\), and the surfaces \(z=f_1(x,y)\) and \(z=f_2(x,y)\), where \(a |
【本文地址】